Exploration statistique

Objectifs du cinquième volet

Ce cinquième volet explore quelques méthodes statistiques d’exploration des données. Le but est d’initier au dialogue entre des traitements géomatiques et l’application de méthodes statistiques pour répondre à une question. Ici, la question va être : les communes traversées par un grand cours d’eau sont-elles en moyenne plus peuplées que les communes non traversées par un grand cours d’eau ? Nous établirons cette différence ou non au moyen d’un test statistique pertinent. À l’issue de ce quatrième volet, vous serez capables d’effectuer les manipulations suivantes :

  • tracer quelques graphiques de présentation des données
  • vérifier la normalité de vos populations par des méthodes graphiques
  • tester la différence de variances entre deux populations par le test de Fisher
  • tester la différence entre deux moyennes en utilisant le test t de Student
  • tester la différence entre deux moyennes en utilisant le test test de Mann-Whitney-Wilcoxon

Données fournies

Pour cet exercice, nous utiliserons les données fournies suivantes :

  • la couche des communes avec leur population (comm_pop.gpkg cf première partie)
  • la couche vecteur des grands cours d’eau (hydro_France.gpkg)

Extraction des données à comparer

Les communes traversées par des cours d’eau ont déjà été extraites dans la première partie. Si besoin, nous pouvons les recharger. Nous pouvons calculer leur population moyenne en interrogeant l’attribut qui contient les populations.

library(terra)
# import des communes traversées par des cours d'eau
comm_hydro <- vect('./Data_processed/communes_hydro.gpkg')
# calcul de la population moyenne
pop_hydro_moy <- mean(comm_hydro$POPULATION)
# import des communes avec les populations
comm_pop <- vect('./Data_processed/communes_France_pop.gpkg')

En moyenne, les communes traversées par des cours d’eau ont une population de 2941.45 habitants.

Pour sélectionner les communes qui ne sont pas traversées par un cours d’eau il y a plusieurs façons de procéder. Ici, nous allons extraire de la couche de toutes les communes, les communes qui ne sont pas dans la couche des communes traversées par un cours d’eau. Cette manipulation va se faire à l’aide d’une fonction de la librairie dplyr nommée anti_join.

library(dplyr)
# nous commençons par extraire les tables d'attributs en dataframe (dplyr ne gère pas les spatVector de terra)
df1 <- as.data.frame(comm_pop)
df2 <- as.data.frame(comm_hydro)

# nous identifions les lignes à garder
lignes_a_garder <- anti_join(df1, df2, by = "INSEE_COM")

# nous récupérons les indices de ces lignes
indices <- which(df1$INSEE_COM %in% lignes_a_garder$INSEE_COM)

# on extrait du spatVector de toutes les communes les lignes qui sont à garder
comm_pas_hydro <- comm_pop[indices]
plot(comm_pas_hydro)

À vous de jouer

Remplacez cette méthode d’extraction par une sélection spatiale.

Nous pouvons maintenant calculer la moyenne de population des communes non traversées par un cours d’eau.

# calcul de la population moyenne
pop_pas_hydro_moy <- mean(comm_pas_hydro$POPULATION)

En moyenne, les communes non traversées par des cours d’eau ont une population de 1228.17 habitants. Nous avons ainsi maintenant les données nécessaires pour tester notre hypothèse.

Tester la normalité des populations

Avant d’appliquer un test t de Student, il est nécessaire de tester la normalité de ces données (comme la plupart des tests statistiques).

Normalité

Dans les faits le test de Student, appliqué sur des échantillons de plus de 30 individus a la réputation d’être robuste même si la normalité n’est pas respectée.

Une méthode couramment utilisée est de regarder la forme de la distribution de ces données. La première chose à faire est de tracer l’histogramme de ces données afin de vérifier que la distribution suit grossièrement la forme d’une cloche. Nous allons utiliser la librairie plotly qui produit facilement des graphiques de bonne facture.

library(plotly)
# histogramme des communes sur un cours d'eau
fig <- plot_ly(x = comm_hydro$POPULATION,
              type = "histogram")
fig

La distribution des populations des communes traversées par un cours d’eau ne suit absolument pas une loi normale. Près de 9000 de ces communes ont une population inférieures à 3000 habitants. Mais faisons confiance à la robustesse du test de Student !

À vous de jouer

Tracez l’histogramme des populations des communes non traversées par un cours d’eau. Qu’en déduisez-vous ?

En plus des histogrammes, pour vérifier la normalité, il est d’usage de tracer ce qu’on appelle le QQ Plot (Quantile-quantile plot). Commençons par tracer celui des communes traversées par un cours d’eau.

# graphique du QQ plot des populations des communes traversées par un cours d'eau
qqnorm(comm_hydro$POPULATION)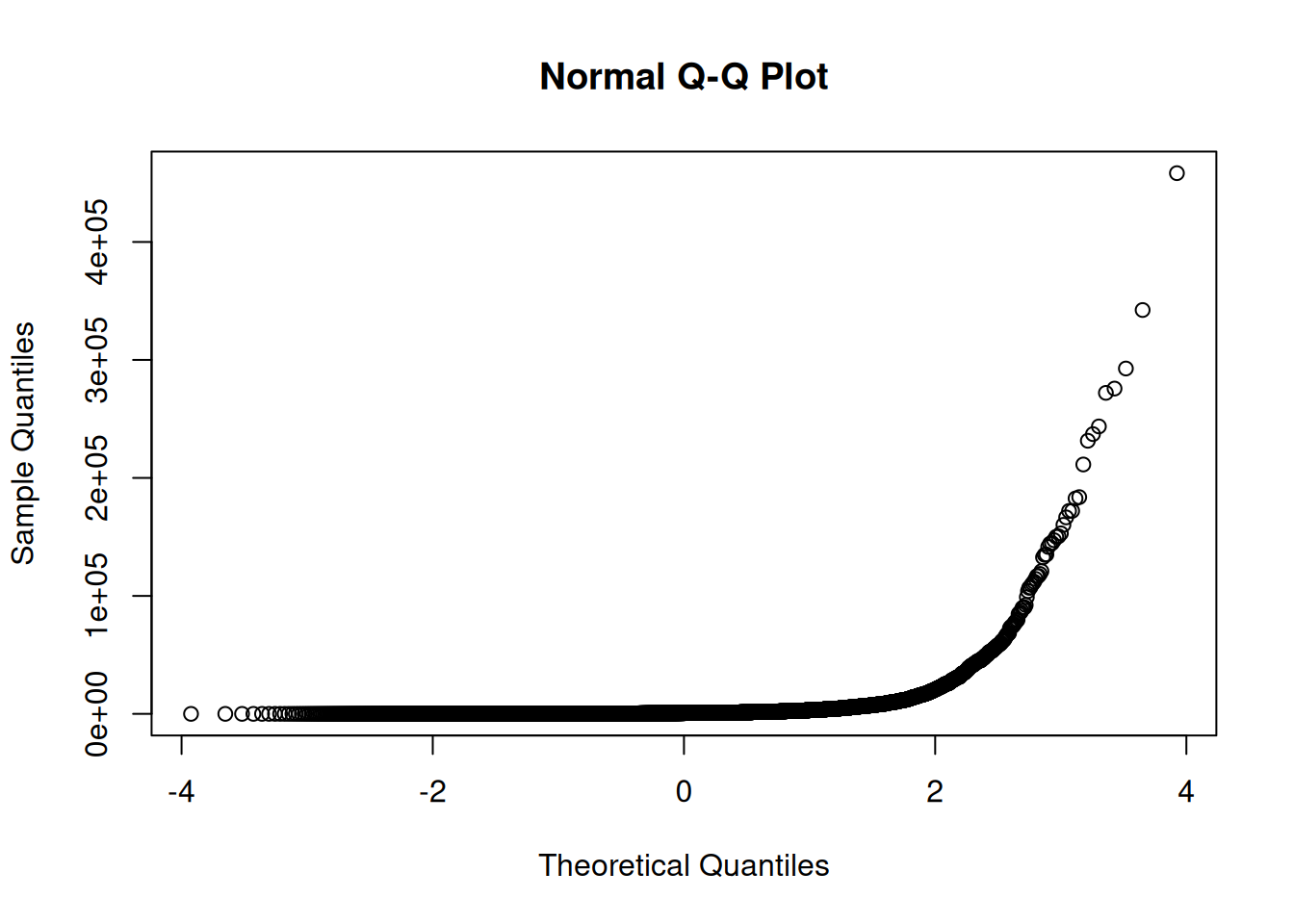

Faisons de même pour les communes non traversées par un cours d’eau.

# graphique du QQ plot des populations des communes non traversées par un cours d'eau
qqnorm(comm_pas_hydro$POPULATION)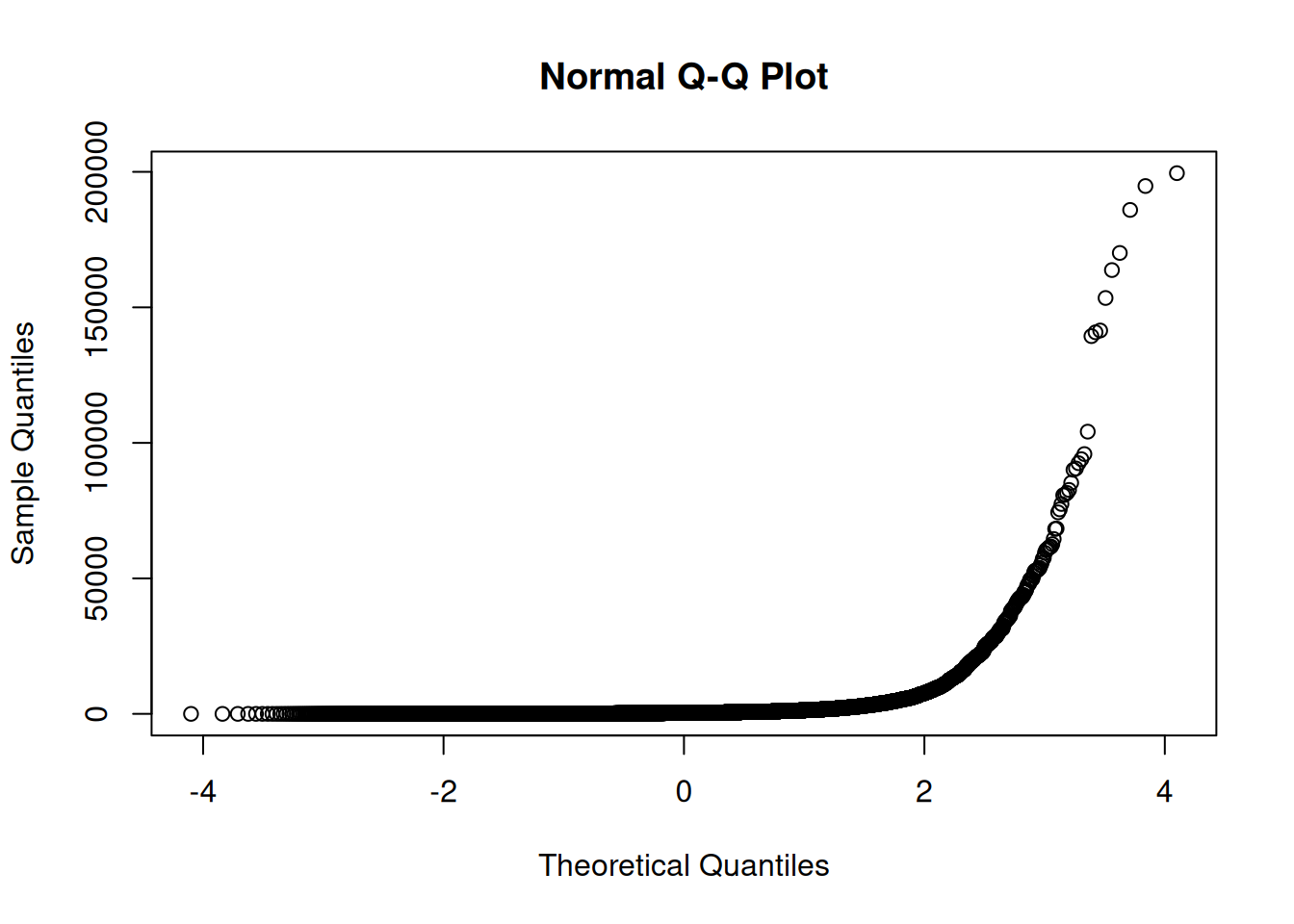

Nous avons ainsi une confirmation que nos échantillons ne suivent pas du tout une loi normale. Appliquons tout de même le test de Student, mais gardons cette non normalité en tête.

Application du test de Fisher

Avant de se lancer dans la comparaison des moyennes, il est nécessaire de vérifier si les variances des deux populations sont égales ou non. La réponse à cette question nous fera utiliser soit un test de Welsh (si les variances sont différentes) soit un test de Student (t-test) (si les variances ne sont pas différentes). Pour tester l’égalité des variances, nous utilisons le test de Fisher. Ce test pose les hypothèses suivantes :

  • H0 : les variances des deux populations ne sont pas significativement différentes
  • H1 : les variances des deux populations sont significativement différentes

Si à l’issue de ce test nous obtenons une p-value inférieure à 0.05, nous rejetons H0 et nous pouvons conclure que les variances sont significativement différentes. Au contraire, si la p-value est supérieure à 0.05 alors nous pouvons accepter H0 et conclure que les deux variances ne sont pas significativement différentes. Ce test se met en oeuvre simplement avec R avec la fonction var.test().

# test de Fisher sur nos deux populations
var.test(comm_hydro$POPULATION, comm_pas_hydro$POPULATION)

    F test to compare two variances

data:  comm_hydro$POPULATION and comm_pas_hydro$POPULATION
F = 5.8265, num df = 11516, denom df = 24280, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 5.647127 6.012698
sample estimates:
ratio of variances 
          5.826528

La p-value est inférieure à 0.05. Nous pouvons donc rejeter H0 et conclure que les variances de nos deux populations sont significativement différentes. Partant de ce résultat, nous allons maintenant utiliser une test de Welch.

Application du test de Student/Welch

Les nombres d’habitants entre les deux types de communes semblent assez différents. Il est donc intéressant de tester la significativité de cette différence via un test statistique. Nos deux variances étant significativement différentes, nous allons utiliser le test de Welch. Ce test va poser deux hypothèses :

  • H0 : les moyennes des deux populations ne sont pas significativement différentes
  • H1 : les moyennes des deux populations sont significativement différentes

Si à l’issue de ce test nous obtenons une p-value inférieure à 0.05, nous rejetons H0 et nous pouvons conclure que les moyennes sont significativement différentes. Pour utiliser un test de Welch, il suffit de préciser var.equal = False dans la fonction t-test.

# application du test de Welch
t.test(comm_hydro$POPULATION, comm_pas_hydro$POPULATION, var.equal = FALSE)

    Welch Two Sample t-test

data:  comm_hydro$POPULATION and comm_pas_hydro$POPULATION
t = 14.333, df = 13425, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 1478.980 1947.585
sample estimates:
mean of x mean of y 
 2941.451  1228.169

La p-value est inférieure à 0.05. Nous pouvons rejeter H0 et conclure que, en moyenne, la population des communes traversées par des cours d’eau est significativement différente de celle des communes non traversées par des cours d’eau.

Nous pouvons continuer notre exploration et tester si la population des communes traversées par des cours d’eau est significativement plus importante que celle des communes non traversées. Pour cela, il suffit de refaire ce t.test en mettant les communes traversées en premier et en ajoutant l’option alternative = “greater”. Avec cette configuration, nous posons les hypothèses suivantes :

  • H0 : la première moyenne est inférieure à la seconde
  • H1 : la première moyenne est supérieure à la seconde
# application du test de Welch pour tester si la moyenne est plus grande avec l'hydro
t.test(comm_hydro$POPULATION, comm_pas_hydro$POPULATION, var.equal = FALSE, alternative = "greater")

    Welch Two Sample t-test

data:  comm_hydro$POPULATION and comm_pas_hydro$POPULATION
t = 14.333, df = 13425, p-value < 2.2e-16
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 1516.654      Inf
sample estimates:
mean of x mean of y 
 2941.451  1228.169

Nous obtenons une p-value inférieure à 0.05, nous pouvons rejeter H0. Nous concluons que les communes traversées par des cours d’eau sont en moyenne plus peuplées que les communes non traversées.

Application du test de Wicoxon

Bien que le test de Student soit considéré robuste pour les grands échantillons même si ils ne suivent pas une loi normale, il peut être prudent d’appliquer un test non paramétrique. En effet, nos deux populations ne suivent pas du tout une distribution normale (adapté aux échantillons non normaux). Dans ce cas, en toute rigueur, pour comparer les deux populations il faut utiliser le test non paramétrique de Mann-Whitney-Wilcoxon. Ce test compare en fait les médianes plutôt que les moyennes. Ce test pose les mêmes hypothèses que le test de Student, à savoir :

  • H0 : les moyennes des deux populations ne sont pas significativement différentes
  • H1 : les moyennes des deux populations sont significativement différentes

Si à l’issue de ce test, la p-value est inférieure à 0.05 nous rejetons H0. La mise en place de ce test se fait facilement en R avec la fonction wilcox.test().

# test de Wilcoxon
wilcox.test(comm_hydro$POPULATION, comm_pas_hydro$POPULATION)

    Wilcoxon rank sum test with continuity correction

data:  comm_hydro$POPULATION and comm_pas_hydro$POPULATION
W = 178990263, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0

Avec ce test également, la p-value est inférieure à 0.05. Nous pouvons donc conclure que nos deux médianes sont significativement différentes. De plus, tout comme le test de Student, nous pouvons tester si une médiane est significativement supérieure à une autre.

# test de Wilcoxon pour médiane supérieure
wilcox.test(comm_hydro$POPULATION, comm_pas_hydro$POPULATION, alternative = "greater")

    Wilcoxon rank sum test with continuity correction

data:  comm_hydro$POPULATION and comm_pas_hydro$POPULATION
W = 178990263, p-value < 2.2e-16
alternative hypothesis: true location shift is greater than 0

La p-value est inférieure à 0.05, les communes traversées par un cours d’eau ont donc une médiane de population significativement supérieure à celle des communes non traversées par un cours d’eau.