Géotraitements et rasters 2

Objectifs du troisième volet

Le but de cette troisième partie est de continuer à croiser plusieurs couches vecteurs à l’aide de géotraitements afin d’en tirer des informations supplémentaires, tout en continuant à utiliser des données rasters. À l’issue de ce troisième volet, vous serez capables d’effectuer les manipulations suivantes :

• calculer des statistiques zonales sur un raster par comparaison à une couche vecteur
• calculer un histogramme zonal entre un raster et un vecteur
• automatisation de tâches

Le fil rouge de cette partie sera de caractériser (sommairement) la topographie à l’échelle des départements français. Nous verrons notamment comment calculer des altitudes maximales et moyennes de façon automatique.

Données fournies

Pour cet exercice, nous utiliserons les données fournies suivantes :

• la couche des départements de France métropolitaine (dep_France.gpkg cf première partie)
• un MNT à l’échelle nationale (MNT_GTopo.tif)

Statistiques zonales

Le but de la manipulation suivante est de calculer des statistiques zonales d’altitude par département. Nous allons calculer l’altitude maximale et l’altitude moyenne par département. Nous commençons par charger dans notre script notre couche des départements.

library(terra)
# import des départements si nécessaire (cd première partie)
dep <- vect('./Data_processed/dep_France.gpkg')

Quel est le SCR de cette couche ?

Réponse

Comme vu dans la première partie, il y a une fonction terra pour obtenir le SCR d’une couche.

# SCR de la couche
crs(dep, describe=TRUE)

                   name authority code
1 RGF93 v1 / Lambert-93      EPSG 2154
                                                                                           area
1 France - onshore and offshore, mainland and Corsica (France métropolitaine including Corsica)
                      extent
1 -9.86, 10.38, 41.15, 51.56

La couche est en Lambert 93, ce qui est pertinent pour notre étude. Nous pouvons maintenant charger dans R notre MNT.

# chargement du MNT
mnt <- rast('./Data/MNT_GTopo.tif')
# affichage
plot(mnt)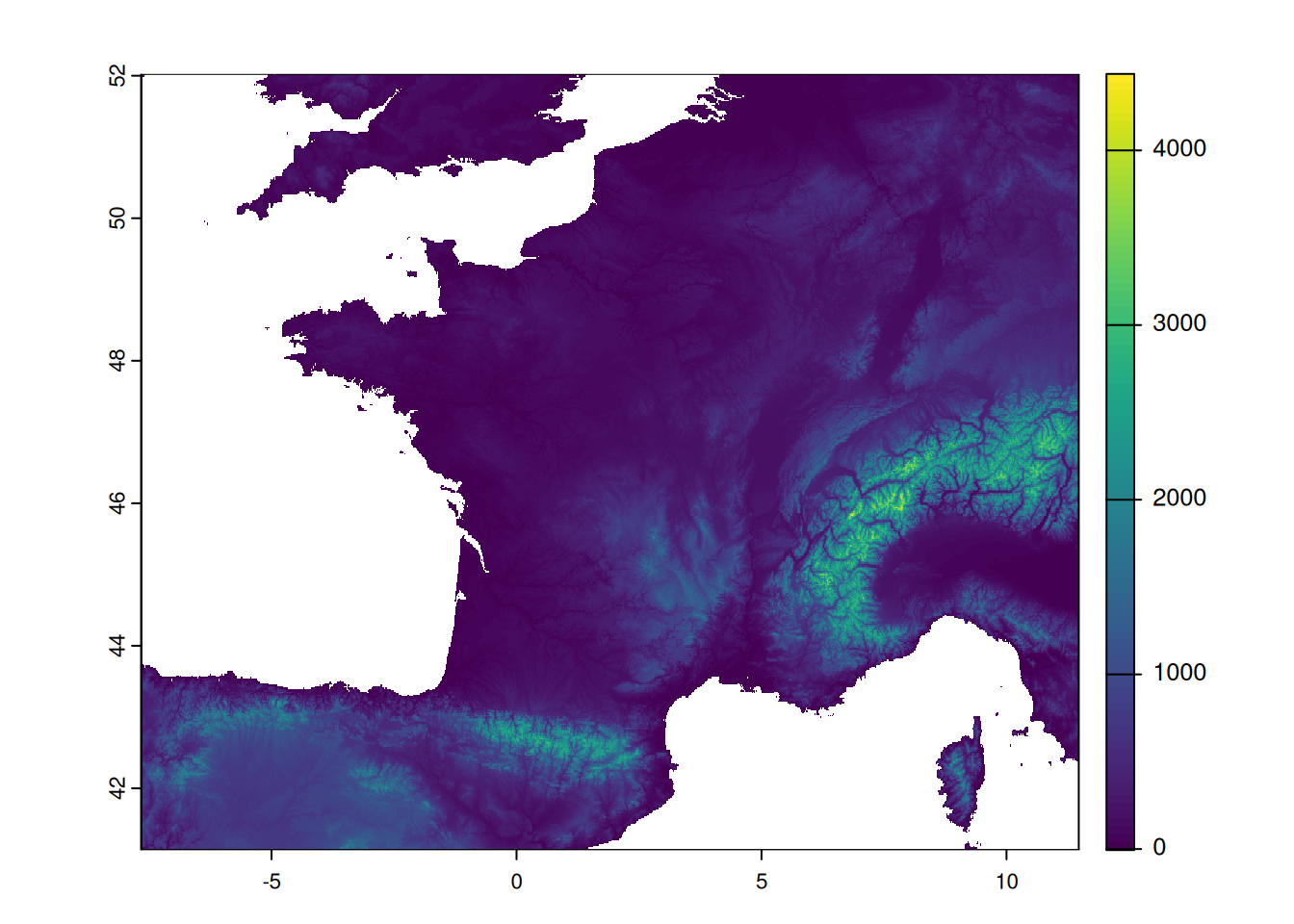

Quel est le SCR de ce raster ? Que préconisez-vous ?

Réponse

De la même façon, il est facile de récupérer le SCR d’un objet raster.

# SCR du raster
crs(mnt, describe=TRUE)

    name authority code  area             extent
1 WGS 84      EPSG 4326 World -180, 180, -90, 90

Ce raster est non projeté, il est en WGS84. Nous allons le projeter dans le système officiel français Lambert 93 afin de pouvoir le croiser avec les départements. Cette reprojection se fait simplement avec la fonction project de terra. Nous verrons ici comment le reprojeter en utilisant le SCR de la couche des départements.

# récupération du code EPSG de la couche des départements
epsg_dep <- crs(dep, describe=TRUE)$code
# reprojection du MNT selon ce code
mnt <- project(mnt, paste0('EPSG:', epsg_dep))

Astuce

La fonction paste0() permet de concatener deux chaînes de caractères sans espaces.

Nous écrasons l’ancienne variable mnt et nous la remplaçons par un nouveau raster dans la bonne projection. Il peut être intéressant de regarder la résolution spatiale de notre MNT.

# résolution spatiale
res(mnt)

[1] 716.3922 716.3922

Le résultat contient deux valeurs, la taille d’un pixel en X et en Y. Ici, un pixel mesure à peu près 716.39 mètres de côté.

Nous pouvons maintenant croiser notre MNT avec les départements. Par exemple, nous allons calculer l’altitude moyenne et maximale par département. La fonction de terra à utiliser est extract. Nous ajoutons l’option na.rm = TRUE afin de ne pas prendre en compte les pixels sans valeurs du raster.

# altitude moyenne et max
dep_alti <- extract(mnt, dep, fun=c('mean', 'max'), bind=TRUE, na.rm = TRUE)

Quel est le point culminant sur le territoire français selon nos données ? Que pouvez-vous en dire ?

Réponse

Le point culminant est la valeur maximale du champ contenant les points culminants par département.

# point culminant
pic_max <- max(dep_alti$max_MNT_GTopo)

Le point culminant de notre MNT s’élève à 4354.76, ce qui ne correspond pas aux 4 805.59 m du Mont Blanc. C’est normal, nous avons ici des pixels qui moyennent l’altitude sur la surface de chaque pixel, à savoir des carrés de 716.39 m par 716.39 m. Donc le pic du Mont Blanc est moyenné avec les altitudes environnantes sur à peu près 50 hectares.

Est-ce-que le département possédant le point culminant du territoire est le même que le département en moyenne le plus haut ?

Réponse

Le département possédant le point maximal le plus haut se trouve en interrogeant la colonne mean_MNT_GTopo.

# extraction du département possédant le point culminant
dep_pic <- dep_alti[dep_alti$max_MNT_GTopo == max(dep_alti$max_MNT_GTopo)]
# récupération du nom du département
dep_pic <- dep_pic$NOM_DEPT

Le département contenant le point culminant est le département de HAUTE-SAVOIE. Le département en moyenne le plus élevé se trouve de façon similaire.

# département en moyenne le plus élevé
dep_moy_pic <- dep_alti[dep_alti$mean_MNT_GTopo == max(dep_alti$mean_MNT_GTopo)]
dep_moy_pic <- dep_alti[dep_alti$mean_MNT_GTopo == max(dep_alti$mean_MNT_GTopo)]$NOM_DEPT

Il s’agît cette fois-ci du département de HAUTES-ALPES.

Discrétiser un raster

Nous allons maintenant voir comment masquer un raster selon un polygone vecteur. Commençons par extraire un département de notre choix.

# extraction d'un département
dep_xtr <- dep[dep$CODE_DEPT == '87']
plot(dep_xtr)

Il faut ensuite enchaîner deux opérations (dans l’ordre de son choix) : le découpage et le masquage. Nous pouvons commencer par découper notre raster selon notre département. C’est-à-dire que nous enlevons du raster tous les pixels qui ne sont pas dans l’emprise de notre polygone de découpe. Ça revient à centrer notre raster. Cela se fait avec la fonction crop de terra.

# découpage du raster
mnt_xtr <- crop(mnt, dep_xtr)
plot(mnt_xtr)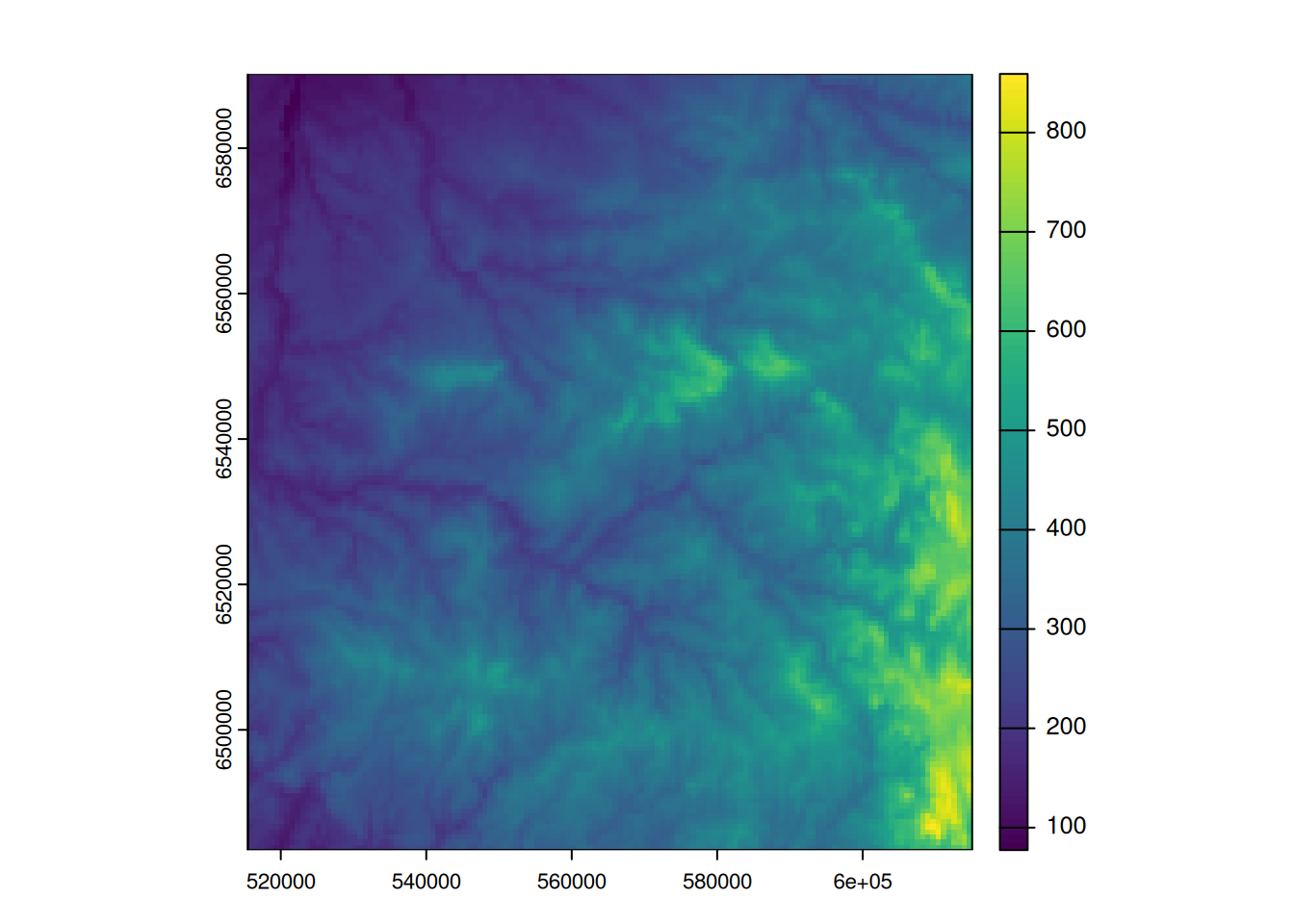

Ensuite nous pouvons masquer ce nouveau raster selon les contours de notre polygone. Ça revient à mettre en no data tous les pixels qui ne sont pas recouverts par ce polygone. Nous utilisons pour ce faire la fonction mask de terra.

# masquage du raster
mnt_xtr <- mask(mnt_xtr, dep_xtr)
plot(mnt_xtr)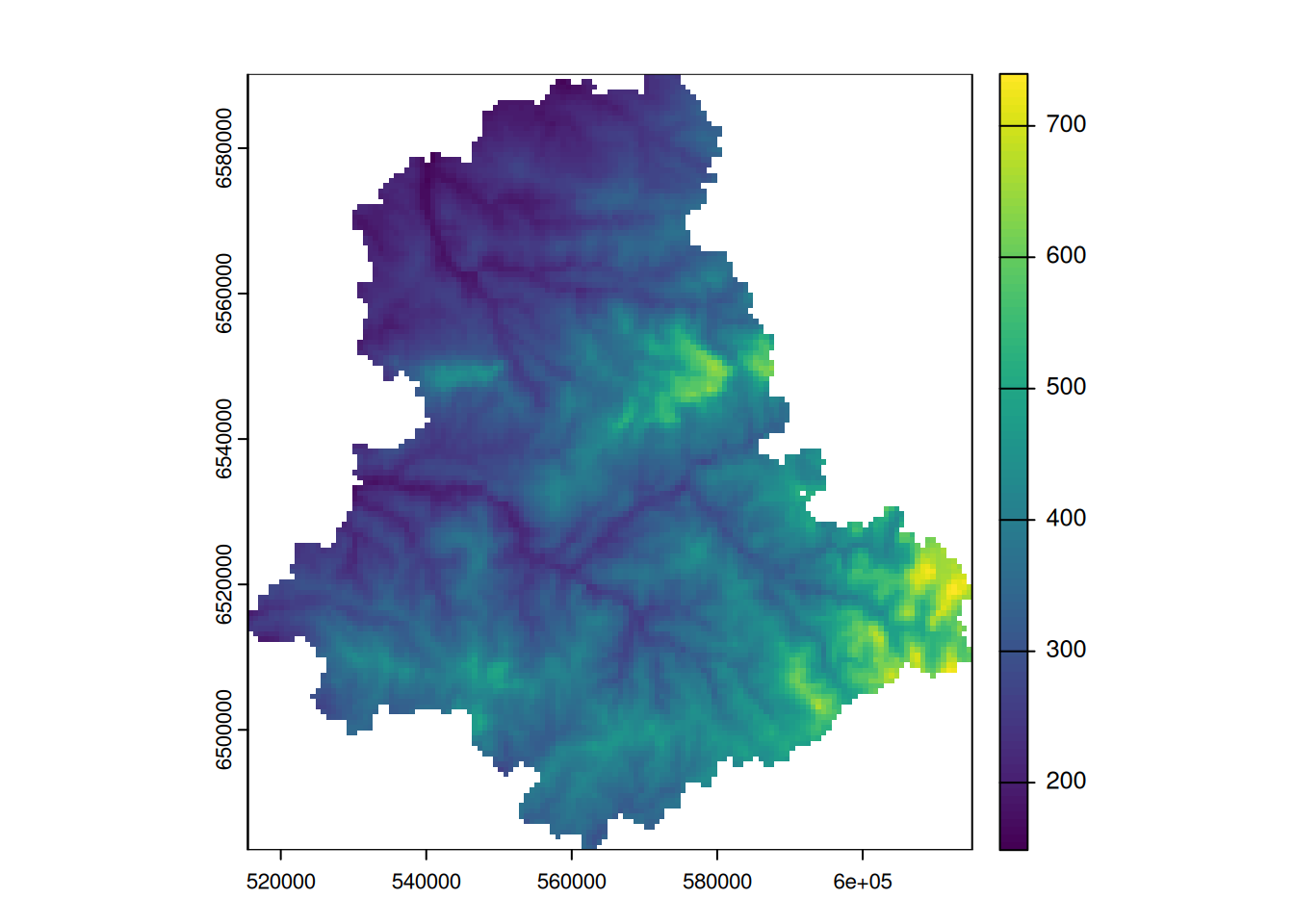

Il est possible d’exporter le résultat sur son disque dur en .tif.

# export du raster
writeRaster(mnt_xtr, './Data_processed/mnt_xtr.tif', overwrite = TRUE)

À vous de jouer

Exercez vous en extrayant et exportant le MNT découpé sur un département de votre choix.

Une fois le MNT extrait sur un département, nous pouvons discrétiser notre raster. Par exemple, nous pouvons facilement créer un raster binaire dans lequel les pixels supérieurs à une certaine altitude seront mis à 1 et les autres à 0. Pour l’exemple, le seuil sera l’altitude moyenne du département. Les pixels supérieurs à la moyenne seront mis à 1 et les pixels inférieurs à la moyenne seront mis à 0.

# calcul de la moyenne du raster
m <- global(mnt_xtr, fun="mean", na.rm = TRUE) 
# création d'un raster binaire
mnt_binaire <- mnt_xtr > m[[1]]
plot(mnt_binaire)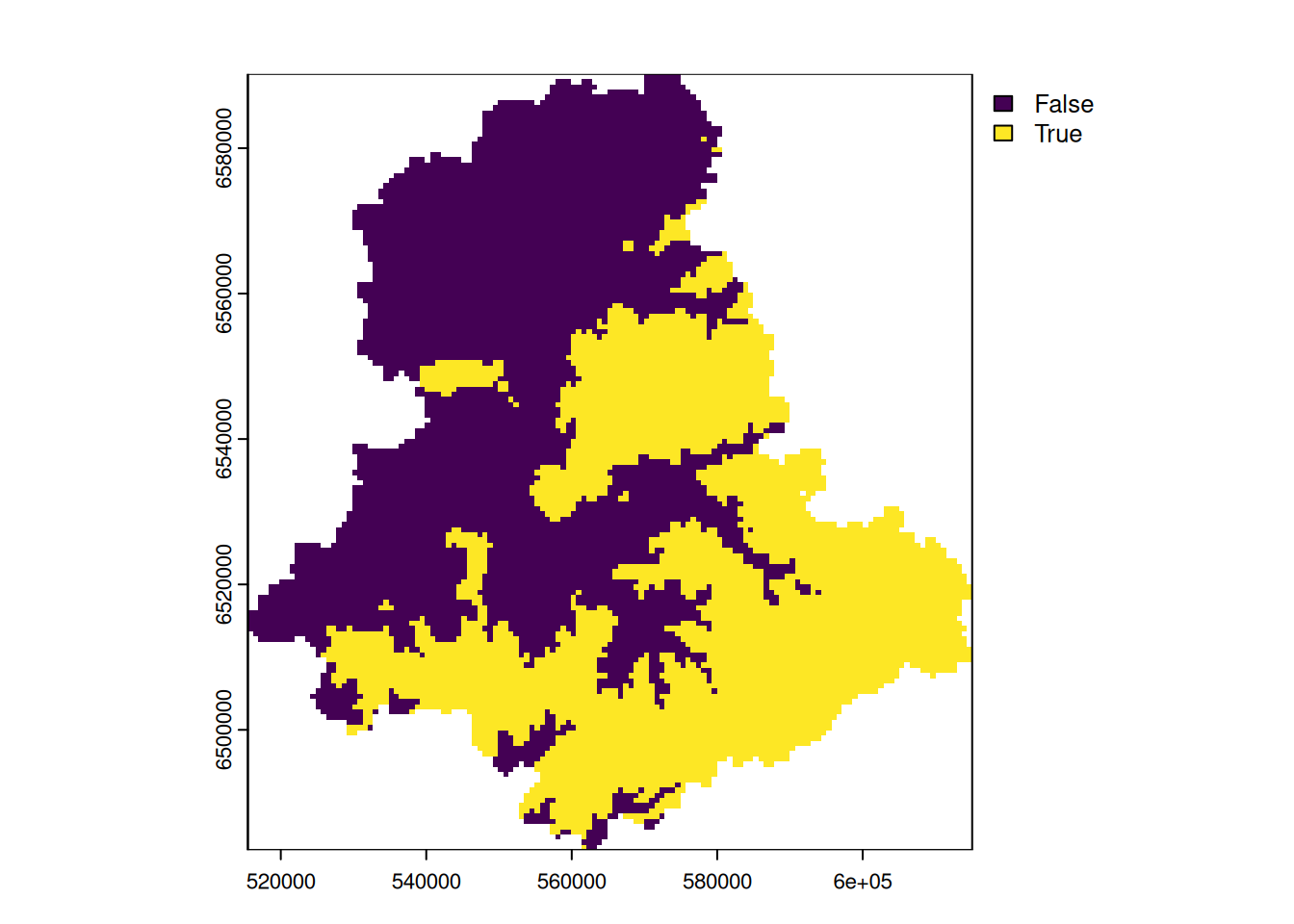

Nous obtenons bien un raster binaire avec des pixels à True (1) et à False (0) selon qu’ils sont supérieurs ou inférieurs au seuil. Nous pouvons compter le nombre de pixels dans l’une ou l’autre catégorie puis multiplier ce nombre de pixels par la résolution spatiale d’un pixel. Nous obtenons ainsi la superficie occupée par ces deux catégories d’altitudes. Ici, nous faisons ce qui est appelé un histogramme zonal.

# superficie d'un pixel (m2)
sup_pix <- res(mnt_binaire)[1] * res(mnt_binaire)[2]
# calcul des fréquences des pixels
f <- freq(mnt_binaire)
# calcul des superficies des classes d'altitude (km2)
sup_alti_0 <- (f$count[f$value == 0] * sup_pix) / 1000000
sup_alti_1 <- (f$count[f$value == 1] * sup_pix) / 1000000

Les altitudes inférieures à la moyenne dans notre département recouvrent ainsi 3113.18 km² et celles supérieures 2660.52 km².

Raster vers vecteur

En SIG il est courant de devoir convertir un fichier raster en fichier vecteur afin de le croiser avec d’autres couches. Cette conversion, aussi appelée vectorisation peut se faire avec la fonction as.polygons de terra. Nous allons ici vectoriser notre raster binaire, afin d’obtenir un polygone correspondant aux surfaces supérieures à l’altitude moyenne et un polygone pour celles inférieures à l’altitude moyenne.

# vectorisation du raster binaire
alti_vect <- as.polygons(mnt_binaire)
plot(alti_vect)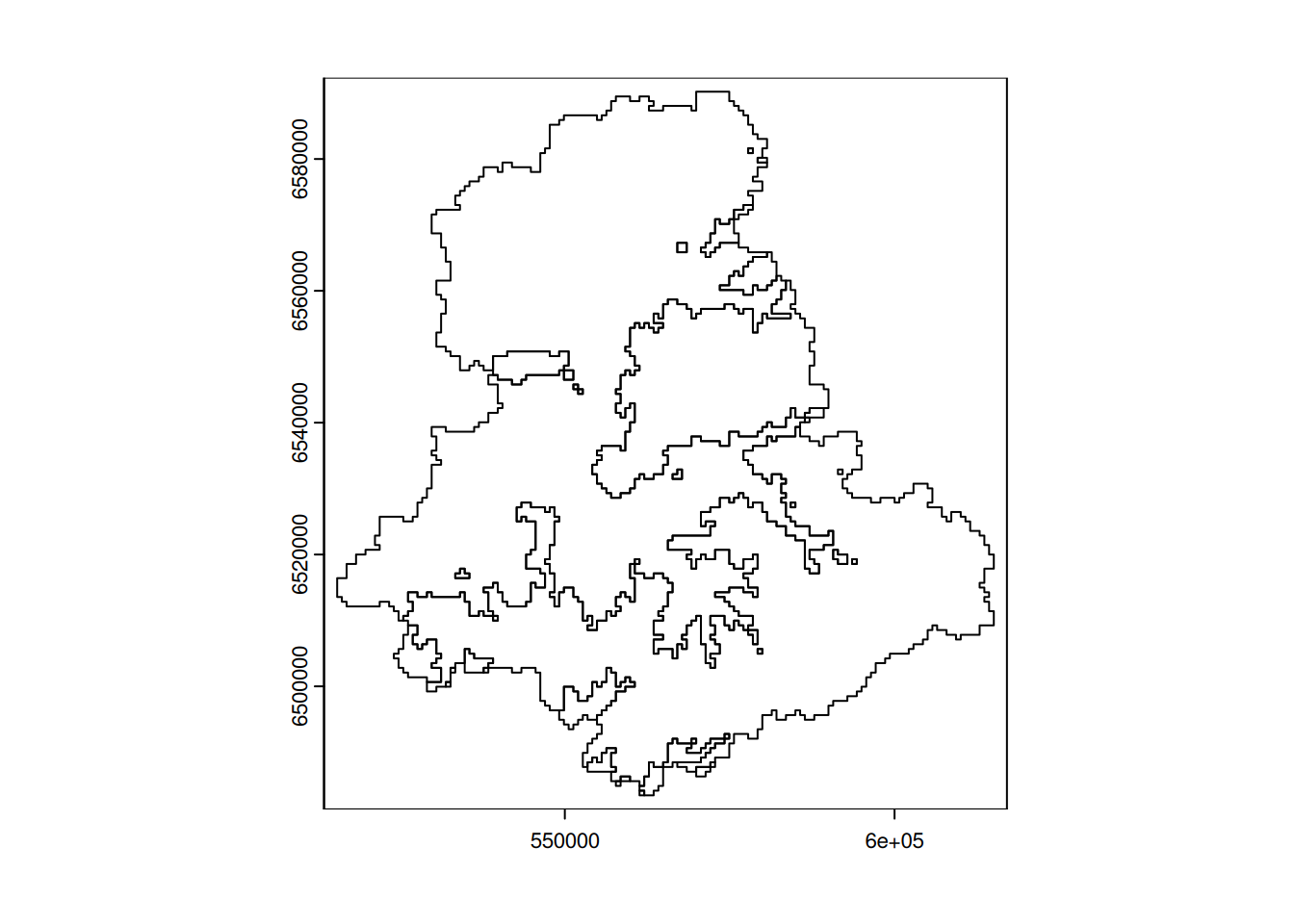

Ajoutez un attribut à cette nouvelle couche dans lequel vous stockez la superficie en kilomètres carrés de chaque zone. Que constatez-vous par rapport aux superficies calculées à partir du raster ?

Réponse

# Ajout d'un attribut de superficie
alti_vect$sup_km2 <- expanse(alti_vect) / 1000000
# affichage de la table attributaire
values(alti_vect)

  MNT_GTopo  sup_km2
1         0 3118.786
2         1 2665.105

Au final, les superficies d’altitudes supérieures à la moyenne recouvrent 2660.52 km² selon la couche raster et 2665.1 km² selon la couche vecteur. Les deux valeurs ne sont pas identiques car, par défaut, la fonction expanse pour une couche vecteur calcule la superficie selon l’ellipsoïde, alors que la résolution du pixel du raster est donné dans la projection du raster. La projection est ici du Lambert 93, projection conforme qui ne conserve pas les surfaces.

Automatisation

L’intérêt d’utiliser un langage de programmation est de pouvoir automatiser une tâche. Par exemple, ce que nous avons fait pour un département, nous pouvons le faire tourner sur l’ensemble des départements de notre couche département pour sortir un raster de MNT par département.

Dans un premier temps, nous pouvons afficher un à un tous les contours des départements. Vous pourrez explorer les contours en parcourant les graphiques dans votre panneau Plots de RStudio.

for(i in 1:length(dep)){
  plot(dep[i])
}

Il suffit maintenant de changer le plot par ce que nous souhaitons faire, par exemple découper et masquer le MNT pour chaque département.

# découpage du MNT par département
for(i in 1:length(dep)){
  mnt_loop <- crop(mnt, dep[i])
  mnt_loop <- mask(mnt_loop, dep[i])
  plot(mnt_loop)
}

En changeant la ligne plot(mnt_loop), nous pourrions sauvegarder le résultat de chaque découpage sur le disque dur.